Bootstrapping

Based on Chapter 8 of ModernDive. Code for Quiz 12.

Load the R package we will use.

library(tidyverse)
library(moderndive)
library(infer)
library(fivethirtyeight)

• Replace all the instances of ???. These are answers on your moodle quiz.
• Run all the individual code chunks to make sure the answers in this file correspond with your quiz answers
• After you check all your code chunks run then you can knit it. It won’t knit until the ??? are replaced
• Save a plot to be your preview plot
• Look at the variable definitions in congress_age

What is the average age of members that have served in congress?

• Set random seed generator to 123
• Take a sample of 100 from the dataset congress_age and assign it to congress_age_100

set.seed(123)
congress_age_100 <- congress_age  %>% 
  rep_sample_n(size=100)

• congress_age is the population and congress_age_100 is the sample

• 18,635 is the number of observations in the population, and 100 is the number of observations in your sample

Construct the confidence interval

1. Use specify to indicate the variable from congress_age_100 that you are interested in

congress_age_100  %>% 
  specify(response = age)

Response: age (numeric)
# A tibble: 100 × 1
     age
   <dbl>
 1  53.1
 2  54.9
 3  65.3
 4  60.1
 5  43.8
 6  57.9
 7  55.3
 8  46  
 9  42.1
10  37  
# … with 90 more rows

---

2. Generate 1000 replicates of your sample of 100

congress_age_100  %>% 
  specify(response = age)  %>% 
  generate(reps = 1000, type= "bootstrap")

Response: age (numeric)
# A tibble: 100,000 × 2
# Groups:   replicate [1,000]
   replicate   age
       <int> <dbl>
 1         1  42.1
 2         1  71.2
 3         1  45.6
 4         1  39.6
 5         1  56.8
 6         1  71.6
 7         1  60.5
 8         1  56.4
 9         1  43.3
10         1  53.1
# … with 99,990 more rows

The output has 99,990 more rows

---

3. Calculate the mean for each replicate

• Assign to bootstrap_distribution_mean_age
• Display bootstrap_distribution_mean_age

bootstrap_distribution_mean_age  <- congress_age_100  %>% 
  specify(response = age)  %>% 
  generate(reps = 1000, type = "bootstrap")  %>% 
  calculate(stat = "mean")

• The bootstrap_distribution_mean_age has 990 means

---

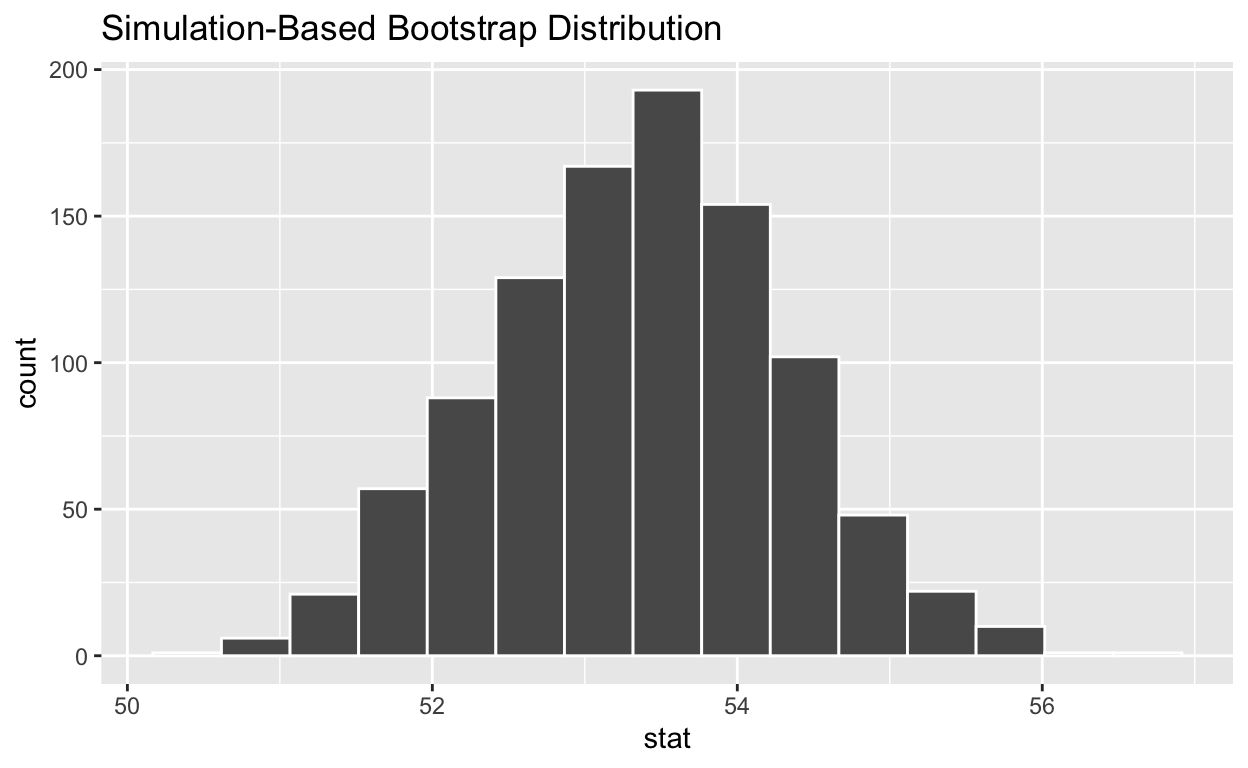
4. Visualize the bootstrap distribution

visualize(bootstrap_distribution_mean_age) 

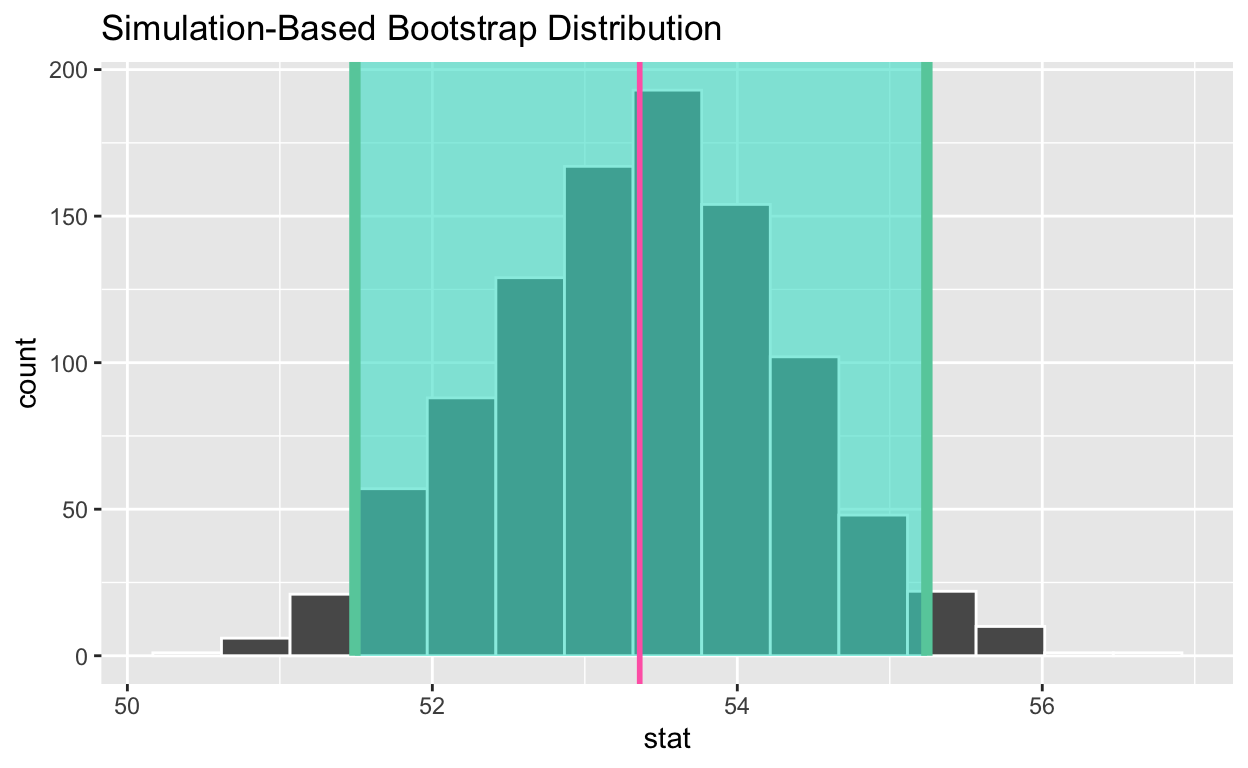
Calculate the 95% confidence interval using the percentile method

• Assign the output to congress_ci_percentile
• Display congress_ci_percentile

congress_ci_percentile  <- bootstrap_distribution_mean_age %>% 
  get_confidence_interval(type = "percentile", level = 0.95)

congress_ci_percentile

# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1     51.5     55.2

Calculate the observed point estimate of the mean and assign it to obs_mean_age

• Display obs_mean_age,

obs_mean_age  <-  congress_age_100  %>% 
  specify(response = age)  %>% 
  calculate(stat = "mean")  %>% 
  pull()

obs_mean_age

[1] 53.36

• Shade the confidence interval
• Add a line at the observed mean, obs_mean_age, to your visualization and color it “hotpink”

visualize(bootstrap_distribution_mean_age) +
  shade_confidence_interval(endpoints = congress_ci_percentile) + 
  geom_vline(xintercept = obs_mean_age, color = "hotpink", size = 1 )

• Calculate the population mean to see if it is in the 95% confidence interval
• Assign the output to pop_mean_age
• Display pop_mean_age

pop_mean_age  <- congress_age  %>% 
  summarize(pop_mean= mean(age))  %>% pull()

pop_mean_age

[1] 53.31373

• Add a line to the visualization at the, population mean, pop_mean_age, to the plot color it “purple”

visualize(bootstrap_distribution_mean_age) +
  shade_confidence_interval(endpoints = congress_ci_percentile) + 
   geom_vline(xintercept = obs_mean_age, color = "hotpink", size = 1) +
   geom_vline(xintercept = pop_mean_age, color = "purple", size = 3)

ggsave(filename = "preview.png", 
       path = here::here("_posts", "2022-04-26-bootstrapping"))

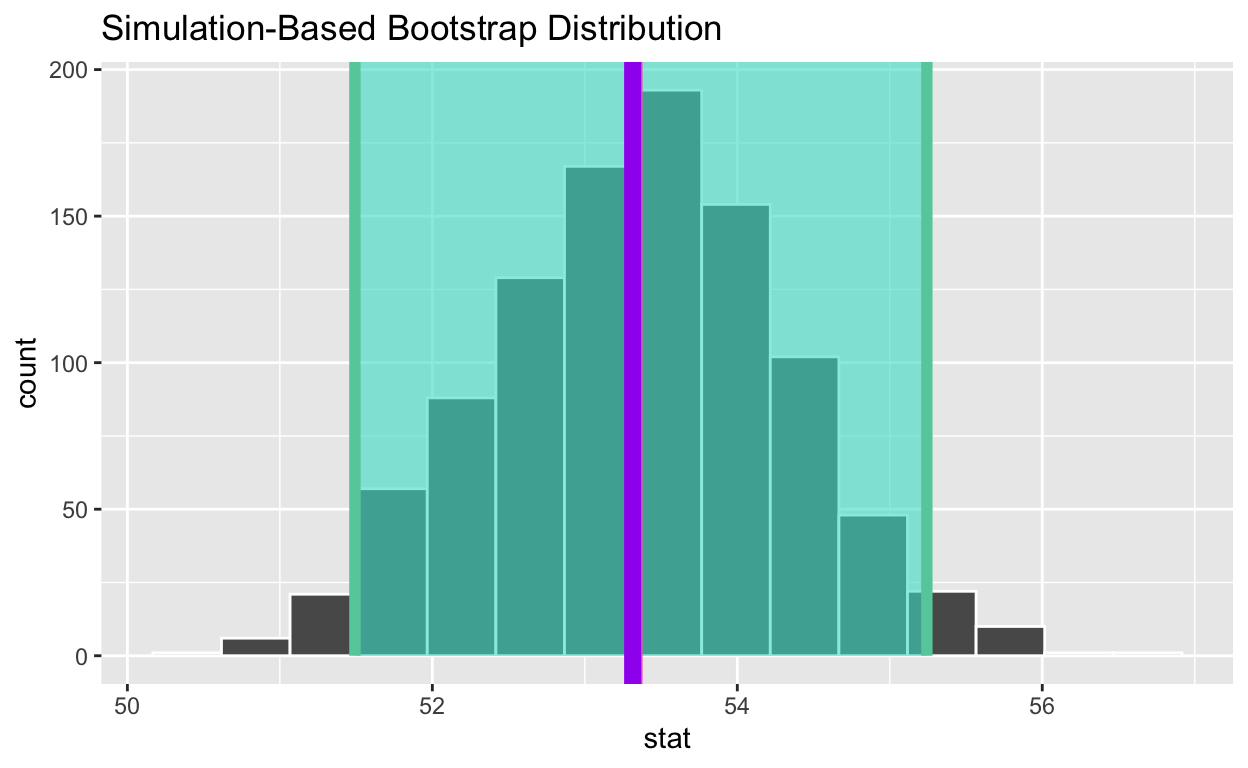
• Is population mean the 95% confidence interval constructed using the bootstrap distribution? Yes.

• Change set.seed(123) to set.seed(4346). Rerun all the code.

  • When you change the seed is the population mean in the 95% confidence interval constructed using the bootstrap distribution? No. 
  • If you construct 100 95% confidence intervals approximately how many do you expect will contain the population mean? 95