Load the R package we will use.

library(tidyverse)
library(moderndive)

Quiz questions

Replace all the instances of ‘SEE QUIZ’. These are inputs from your moodle quiz.
Replace all the instances of ‘???’. These are answers on your moodle quiz.
Run all the individual code chunks to make sure the answers in this file correspond with your quiz answers
After you check all your code chunks run then you can knit it. It won’t knit until the ??? are replaced
The quiz assumes that you have watched the videos and worked through the examples in Chapter 7 of ModernDive

Question:

7.2.4 in Modern Dive with different sample sizes and repetitions

Make sure you have installed and loaded the tidyverse and the moderndive packages
Fill in the blanks
Put the command you use in the Rchunks in your Rmd file for this quiz.

Modify the code for comparing different sample sizes from the virtual bowl

Segment 1: sample size = 30

1a) Take 1200 samples of size of 30 instead of 1000 replicates of size 25 from the bowl dataset. Assign the output to virtual_samples_30

virtual_samples_30  <- bowl  %>% 
rep_sample_n(size = 30, reps = 1200)

1b) Compute resulting 1200 replicates of proportion red

start with virtual_samples_30 THEN
group_by replicate THEN
create variable red equal to the sum of all the red balls
create variable prop_red equal to variable red / 30
assign the output to virtual_prop_red_30

virtual_prop_red_30 <- virtual_samples_30 %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 30)

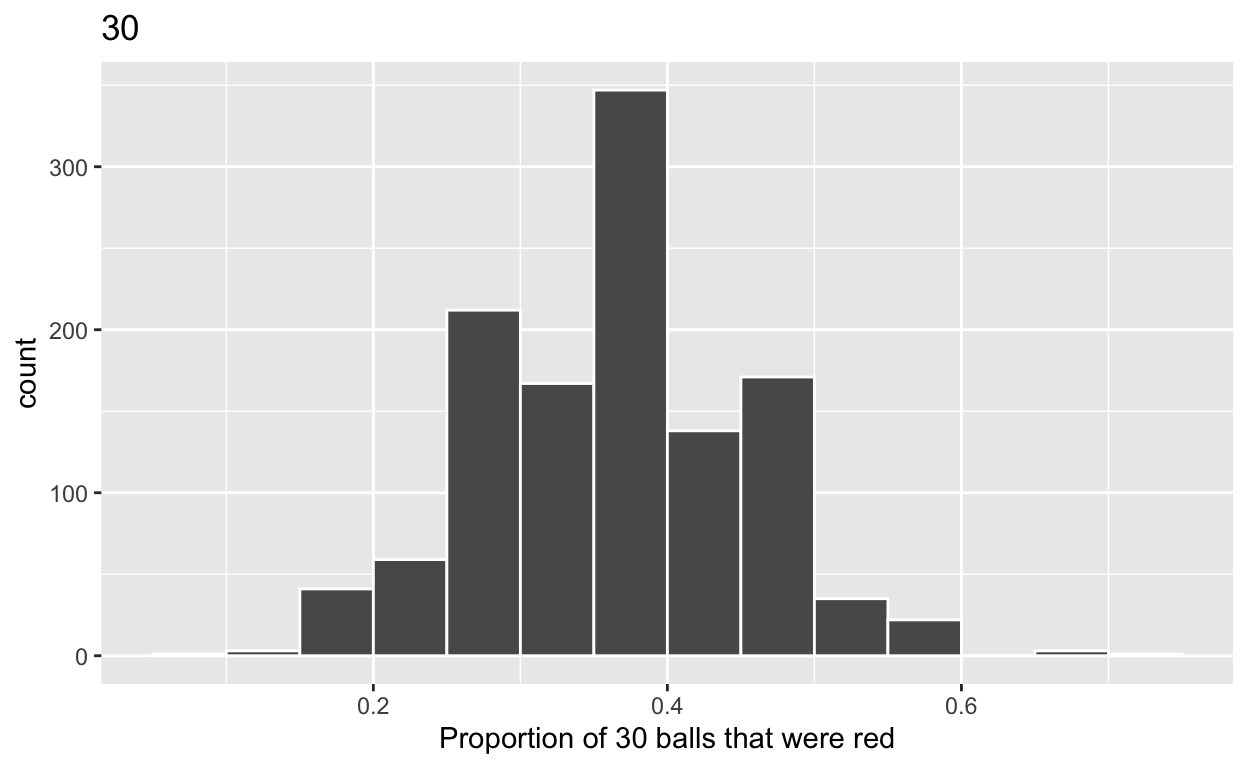
1c) Plot distribution of virtual_prop_red_30 via a histogram

Use labs to:

label x axis = “Proportion of 30 that were red”
create title = “30”

ggplot(virtual_prop_red_30, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 30 balls that were red", title = "30")

Segment 2: sample size = 55

2a) Take 1200 samples of size of 55 instead of 1000 replicates of size 50. Assign the output to virtual_samples_55

virtual_samples_55  <- bowl  %>% 
rep_sample_n(size = 55, reps = 1200)

2b) Compute resulting 55 replicates of proportion red

start with virtual_samples_55 THEN group_by replicate THEN create variable red equal to the sum of all the red balls create variable prop_red equal to variable red / 55 Assign the output to virtual_prop_red_55

virtual_prop_red_55 <- virtual_samples_55 %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 55)

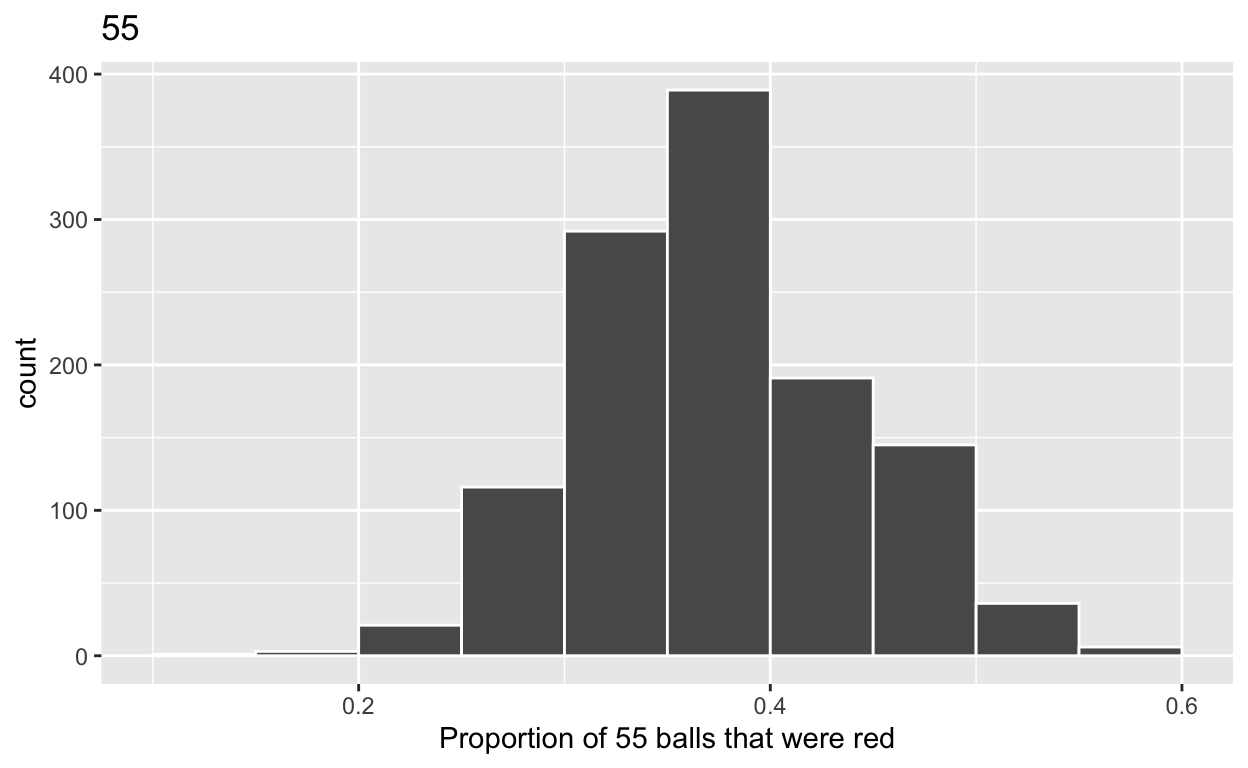
2c) Plot distribution of virtual_prop_red_55 via a histogram use labs to

label x axis = “Proportion of 55 balls that were red”
create title = “55”

ggplot(virtual_prop_red_55, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 55 balls that were red", title = "55")

Segment 3: sample size = 120

3a) Take 1200 samples of size of 120 instead of 1000 replicates of size 50. Assign the output to virtual_samples_120

virtual_samples_120  <- bowl  %>% 
rep_sample_n(size = 120, reps = 1200)

3b) Compute resulting 1200 replicates of proportion red

start with virtual_samples_120 THEN
group_by replicate THEN
create variable red equal to the sum of all the red balls
create variable prop_red equal to variable red / 120
assign the output to virtual_prop_red_120

virtual_prop_red_120 <- virtual_samples_120 %>% 
  group_by(replicate) %>% 
  summarize(red = sum(color == "red")) %>% 
  mutate(prop_red = red / 120)

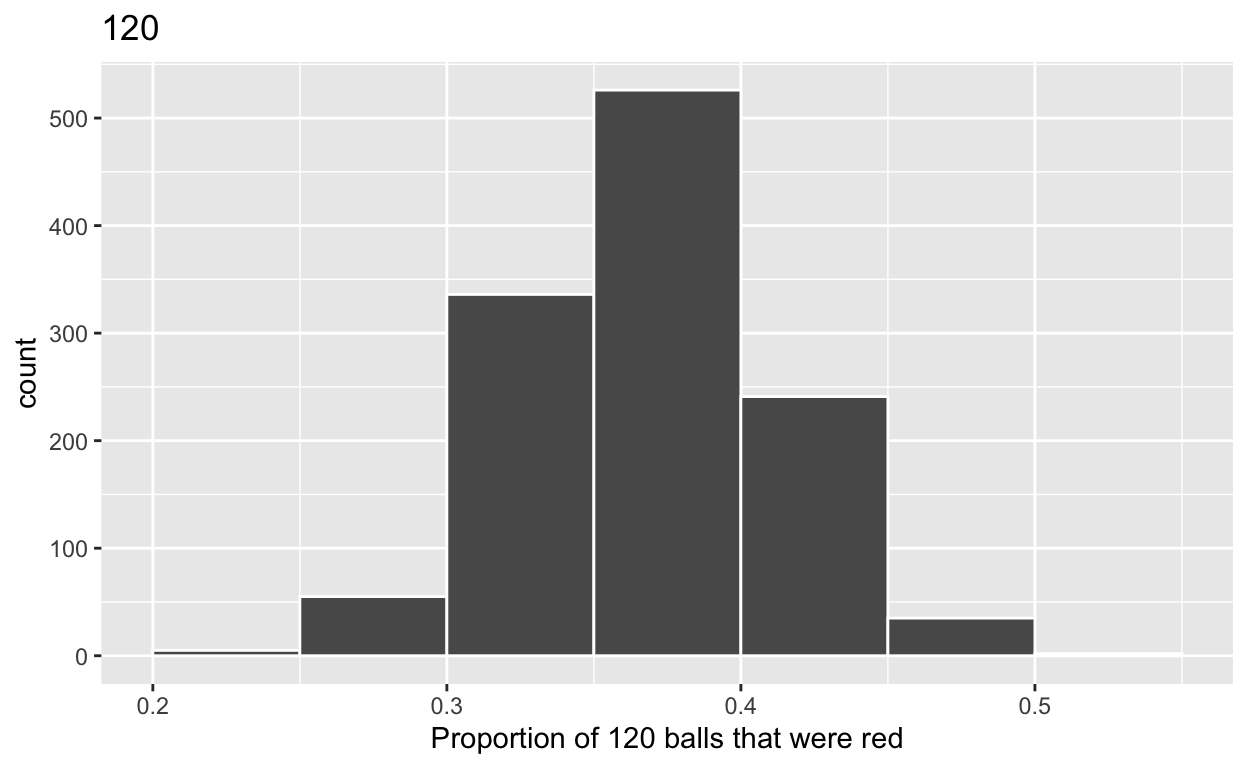
3c) Plot distribution of virtual_prop_red_120 via a histogram

Use labs to:

label x axis = “Proportion of 120 balls that were red”
create title = “120”

ggplot(virtual_prop_red_120, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 120 balls that were red", title = "120")

ggsave(filename = "preview.png", 
       path = here::here("_posts", "2022-04-19-sampling"))

Calculate the standard deviations for your three sets of 1200 values of prop_red using the standard deviation

n = 30

virtual_prop_red_30 %>% 
  summarize(sd = sd(prop_red))

# A tibble: 1 × 1
      sd
   <dbl>
1 0.0890

n = 55

virtual_prop_red_55 %>% 
  summarize(sd = sd(prop_red))

# A tibble: 1 × 1
      sd
   <dbl>
1 0.0657

n = S120

virtual_prop_red_120 %>% 
  summarize(sd = sd(prop_red))

# A tibble: 1 × 1
      sd
   <dbl>
1 0.0429

The distribution with sample size, n = 120, has the smallest standard deviation (spread) around the estimated proportion of red balls.

Sampling

Question: